통계적 데이터 분석 / 모델링 : 회귀분석
상관 분석
두 변수가 어떤 선형적인 관계를 가지고 있는지를 분석하는 방법.
각 변수를 x, y축에 넣고 그 변하는 정도, 상관 계수 (기울기)를 구한다.
상관계수는 -1이상 1이하의 값을 가지며, 0.7 이상일땐 강한 양의 상관관계, -0.7 이하일땐 강한 음의 상관관계를 가진다.

Excel 데이터 분석을 통해 좌측 표의 각 열에 대하여 상관관계를 구하면 우측 표가 된다.
우측 하단 표를 정리하여 조건부 서식으로 시각화한게 우측 상단표.
매출과 각각의 요소는 평균 이상의 상관관계를 보이고 있는데,
그 중에서도 매출과 판매수량의 상관계수가 매우 높다.
또 해당 표에서는 모든 요소들은 양의 상관관계를 가지며 음의 상관관계는 하나도 없다.
그럼 양의 상관관계를 가지는 두 관계는 반드시 인과관계가 있는가?
그렇지 않다.
하지만 인과관계가 있는 두 변수는 반드시 강한 상관관계를 가진다.
이를 구분하기 위해서는 많은 실험을 통해 입증해야 한다.
공분산
2개의 확률 변수의 선형관계를 나타내는 값으로 0이면 상관관계가 없다고 본다.
음수값이면 음의 상관관계, 양수값이면 양의 상관관계를 가진다고 본다.
단, 두 변수가 아무 관계 없는 독립변수일 때 공분산 = 0 이지만,
공분산이 0 이라고 해서 무조건 두 변수가 독립은 아니다.
아래는 같은 데이터를 가지고 공분산 분석과 상관관계를 분석해 본 결과이다.
SepalLengthCm 와 PetalWidthCm 의 관계는 공분석에서는 높은 계수를 보이지 않지만
상관관계에서는 높은 계수를 보이고 있다.

이 데이터를 산점도로 나타내면 아래와 같다.
추세선 또한 추가해 보면 강한 양의 상관관계를 가지고 있다고 볼 수 있다.
따라서, 상관관계를 보기 위핸 공분산 분석보다는 상관관계분석을 사용하는 쪽을 추천하는 편.

회귀 분석이란?
두 개 이상의 종속변수와 독립변수의 관계를 분석하는 방법 (이때 변수는 연속형 변수)
두 변수 사이의 관계를 파악하면 우리가 알고 싶은 값을 예측할 수 있다는 장점을 가진다.
단 두 변수간의 인과관계를 설명해주진 못한다.
이에 대한 부분은 상관관계 포스팅에서도 다뤘었다.
보통 1차 함수로 표현할 수 있다.
아래는 선형회귀 분석 식으로, 여기서 y값이 종속 변수, x값이 독립변수에 해당한다.
다수의 독립변수는 아래와 같이 항을 증가시켜서 표현할 수 있다.

회귀분석은 2가지로 나눌 수 있다. 선형이냐, 비선형이냐.
여기서 선형회귀분석도 단순 회귀 (독립변수가 하나), 다중회귀 (독립변수가 여러개)로 나눌 수 있다.
- 단순 선형 회귀 분석
엑셀 -데이터 - 데이터 탐색 - 회귀분석 (데이터 선택시 수치로 주어야, 데이터 중 1열을 y값으로 본다)
결정 계수 : 데이터의 신뢰도, 설명도. 아래 그림에서 이 회귀 모형은 실제 데이터의 39.7%를 설명한다.
유의한 F : 0.05 미만이면 이 회귀모형이 유의미하다.
계수들을 통해 1차 함수 식을 만들어 추세선의 식을 구할 수 있다.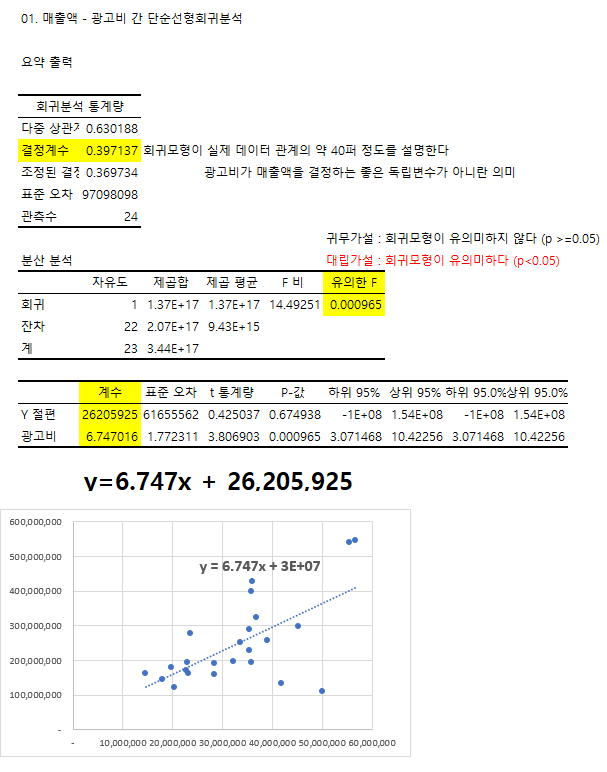
- 다중 선형 회귀 분석
단순선형과 같은 방법으로 구한다. 단 데이터 값을 다중 항목이 포함되도록 한다.
다중선형회귀에선 '조정된 결정계수'를 봐야한다. 1에 가까울 수록 설명도가 높다. 아래는 96.3%의 설명도를 가진다.
유의한 F 값이 0.05 미만이어야 모형이 유의미하다.
각 항목들이 종속변수에 대하여 구한 p값이 0.05 보다 작은 변수들에 주목해야 한다.
0.05보다 작은 변수들이 종속 변수에 영향을 미칠것으로 기대되는 변수들이기 때문이다.